Bài tập Cấu trúc dữ liệu và giải thuật(C++)
Bài 1.Hãy viết chương trình tìm số các số tự nhiên N thỏa mãn đồng thời những điều kiện dưới đây (N<=2^31):
• N là số có K chữ số (K<=15).
• N là số nguyên tố.
• Đảo ngược các chữ số của N cũng là một số nguyên tố.
• Tổng các chữ số của N cũng là một số nguyên tố.
• Mỗi chữ số của N cũng là các số nguyên tố ;
• Thời gian thực hiện chương trình không quá 1sec.
Dữ liệu vào (Input) cho bởi file data.in theo khuôn dạng:
• Dòng đầu tiên ghi lại số tự nhiên M là số lượng các test (M<=100).
• M dòng kế tiếp ghi lại mỗi dòng một test. Mỗi test bao gồm một số K. Hai số được viết cách nhau một vài khoảng trống.
Kết quả ra (Output): ghi lại M dòng trong file ketqua.out, mỗi dòng ghi lại bộ hai số số N, X. Trong đó X là số các số có N chữ số thỏa mãn yêu cầu của bài toán. Ví dự dưới đây minh họa cho file input và output của bài toán.
Input.in Output.out5
2 2 0
3 3 8
4 4 15
5 5 46
7 7 359
Tải về code C++
Bài 2.Cho dãy A[] gồm N số tự nhiên khác nhau và số tự nhiên K. Hãy sử dụng thuật toán sinh viết chương trình liệt kê tất cả các dãy con của dãy số A[] sao cho tổng các phần tử trong dãy con đó đúng bằng K.
Dayso.in Ketqua.out
5 50 3
5 10 15 20 25 10 15 25
5 20 25
5 10 15 20
Tải về code C++Dayso.in Ketqua.out
5 50 3
5 10 15 20 25 10 15 25
5 20 25
5 10 15 20
Bài 3.Cho dãy AN = {a1, a2, ..,aN} gồm N số tự nhiên phân biệt. Hãy sử dụng thuật toán sinh (quay lui, nhánh cận, qui hoạch động) viết chương trình liệt kê tất cả các dãy con K phần tử của dãy số AN (K<=N) sao cho tổng các phần tử của dãy con đó là một số đúng bằng B.
dayso.in ketqau.out
5 3 50 2
5 10 15 20 25 5 20 25
10 15 25
Tải về code C++dayso.in ketqau.out
5 3 50 2
5 10 15 20 25 5 20 25
10 15 25
Bài 4.Hãy sử dụng thuật toán sinh (quay lui, nhánh cận, qui hoạch động) viết chương trình Viết chương trình tìm X = (x1, x2,..,xn) và f(X) đạt giá trị lớn nhất. Trong đó:
Caitui.in Ketqua.out
4 8 15
5 10 1 1 0 0
3 5
2 3
4 6
Tải về code C++4 8 15
5 10 1 1 0 0
3 5
2 3
4 6
Bài 5. Một dãy số tự nhiên bất kỳ AN = {a1, a2,.., aN} được gọi là một dãy số nguyên tố thuần nhất bậc K nếu tổng K phần tử liên tiếp bất kỳ của dãy số AN là một số nguyên tố (K <= N). Ví dụ dãy số AN = {3, 27, 7, 9, 15} là một dãy số nguyên tố thuần nhất bậc 3. Cho dãy số AN. Hãy liệt kê tất cả các dãy số nguyên tố thuần nhất bậc K có thể có được tạo ra bằng cách tráo đổi các phần tử khác nhau của dãy số AN.
Ví dụ:
Input:
• n = 5, K =3
• A = (3, 7, 9, 15, 27)
Output: 4
3 27 7 9 15
15 9 7 3 27
15 9 7 27 3
27 3 7 9 15
Tải về code C++Ví dụ:
Input:
• n = 5, K =3
• A = (3, 7, 9, 15, 27)
Output: 4
3 27 7 9 15
15 9 7 3 27
15 9 7 27 3
27 3 7 9 15
Bài 6. Cho số tự nhiên n. Hãy in ngược lại dãy số tự nhiên ngược lại từ n đến 1. Ví dụ n=5, ta in ngược lại là : 5 4 3 2 1.
Tải về code C++Bài 7. Nâng số tự nhiên x lên lũy thừa n.
Tải về code C++Bài 8. Tìm số fibonacci thứ n.
Tải về code C++Bài 9. Đảo ngược một xâu ký tự.
Tải về code C++Bài 10.Tìm vị trí của x trong dãy số A = { A0, A1, A2, .., An-1}.
Tải về code C++Bài 11.Tìm tổng của các chữ số trong số tự nhiên K.
Tải về code C++Bài 12.Tìm tổng của tất cả các phần tử của dãy số A = { A0, A1, A2, .., An-1}.
Tải về code C++Bài 13.Đổi số tự nhiên n thành số nhị phân.
Tải về code C++Bài 14.Cho tập gồm n hành động, mỗi hành động được biểu diễn như bộ đôi thời gian bắt đầu si và thời gian kết thúc fi (i=1, 2, .., n). Bài toán đặt ra là hãy lựa chọn nhiều nhất các hành động có thể thực hiện bởi một máy hoặc một cá nhân mà không xảy ra tranh chấp. Giả sử mỗi hành động chỉ thực hiện đơn lẻ tại một thời điểm.
Input:- Số lượng hành động: 6
- Thời gian bắt đầu Start []= { 1, 3, 0, 5, 8, 5}
- Thời gian kết thúc Finish[]= { 2, 4, 6, 7, 9, 9}
Output: Số lượng lớn nhất các hành động có thể thực hiện bởi một người.
OPT[] = {0, 1, 3, 4 }
Tải về code C++Input:- Số lượng hành động: 6
- Thời gian bắt đầu Start []= { 1, 3, 0, 5, 8, 5}
- Thời gian kết thúc Finish[]= { 2, 4, 6, 7, 9, 9}
Output: Số lượng lớn nhất các hành động có thể thực hiện bởi một người.
OPT[] = {0, 1, 3, 4 }
Bài 15.Bài toán n-ropes. Cho n dây với chiều dài khác nhau. Ta cần phải nối các dây lại với nhau thành một dây. Chi phí nối hai dây lại với nhau được tính bằng tổng độ dài hai dây. Nhiệm vụ của bài toán là tìm cách nối các dây lại với nhau thành một dây sao cho chi phí nối các dây lại với nhau là ít nhất.
Input: - Số lượng dây: 4
- Độ dài dây L[]= { 4, 3, 2, 6}
Output: Chi phí nối dây nhỏ nhất.
OPT = 39
Tải về code C++Input: - Số lượng dây: 4
- Độ dài dây L[]= { 4, 3, 2, 6}
Output: Chi phí nối dây nhỏ nhất.
OPT = 39
Bài 16.Cho xâu ký tự s[] độ dài n và số tự nhiên d. Hãy sắp đặt lại các ký tự trong xâu s[] sao cho hai ký tự giống nhau đều cách nhau một khoảng là d. Nếu bài toán có nhiều nghiệm, hãy đưa ra một cách sắp đặt đầu tiên tìm được. Nếu bài toán không có lời giải hãy đưa ra thông báo “Vô nghiệm”.
Ví dụ.
Input:
• Xâu ký tự S[] =“ABB”;
• Khoảng cách d = 2.
Output: BAB
Input:
• Xâu ký tự S[] =“AAA”;
• Khoảng cách d = 2.
Output: Vô nghiệm.
Input:
• Xâu ký tự S[] =“GEEKSFORGEEKS”;
• Khoảng cách d = 3.
Output: EGKEGKESFESOR.
Tải về code C++Ví dụ.
Input:
• Xâu ký tự S[] =“ABB”;
• Khoảng cách d = 2.
Output: BAB
Input:
• Xâu ký tự S[] =“AAA”;
• Khoảng cách d = 2.
Output: Vô nghiệm.
Input:
• Xâu ký tự S[] =“GEEKSFORGEEKS”;
• Khoảng cách d = 3.
Output: EGKEGKESFESOR.
Bài 17.Cho dãy số nguyên bao gồm cả số âm lẫn số dương. Nhiệm vụ của ta là tìm dãy con liên tục có tổng lớn nhất.
Ví dụ. Với dãy số A = {-2, -5, 6, -2, -3, 1, 5, -6} thì tổng lớn nhất của dãy con liên tục ta nhận được là 7.
Tải về code C++Ví dụ. Với dãy số A = {-2, -5, 6, -2, -3, 1, 5, -6} thì tổng lớn nhất của dãy con liên tục ta nhận được là 7.
Bài 18.Cho mảng số nguyên 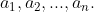 .Tìm cặp số có hiệu độ lệch lớn nhất trong đó số lớn hơn đứng ở sau số nhỏ hơn.Giả sử Diff(a[1,n]) độ lệch cần tìm thì Diff(a[1,n])=Max(
.Tìm cặp số có hiệu độ lệch lớn nhất trong đó số lớn hơn đứng ở sau số nhỏ hơn.Giả sử Diff(a[1,n]) độ lệch cần tìm thì Diff(a[1,n])=Max(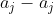 ) trong đó 1<=i<=j<=n.
) trong đó 1<=i<=j<=n.
Tải về code C++(Giải thuật chia để trị)
Bài 19.Trong giờ học môn Điện tử số về mã Gray, MĐ chợt nảy sinh ra một bài toán để code. Bài toán rất đơn giản như sau: In ra lần lượt bảng mã gray n-bit.
Mã Gray là mã nhị phân mà hai mã liền kề trong bảng mã chỉ khác nhau một bit. Các giá trị ở nửa sau của bảng mã có sự đối xứng với nửa đầu của bảng mã theo thứ tự ngược lại, ngoại trừ bit cao nhất bị đảo giá trị (bit cao nhất là bit ngoài cùng bên trái). Tính chất đối xứng này vẫn đúng cho các bit thấp hơn trong mỗi nửa, mỗi phần tư,… của bảng mã.
Input
Một số nguyên duy nhất n (1<=n<=16).
Output
Bảng mã gray n-bit theo thứ tự, mỗi mã trên một dòng.
Tải về code C++
Bài 20.Cho số tự nhiên X.Hãy tìm cách biểu diễn X thành tổng lũy thừa bậc n của các số tự nhiên khác nhau.
Input: Output:
X=10,n=2 1 3
X=100,n=2 0 10
6 8
Tải về code C++
Bài 21.1. Special Triangle [A]. Cho dãy số A[] gồm n số nguyên dương. Tam giác đặc biệt của dãy số A[] là tam giác được tạo ra bởi n hàng, trong đó hàng thứ n là dãy số A[], hàng i là tổng hai phần tử liên tiếp của hàng i+1 (1≤i≤n-1). Ví dụ A[] = {1, 2, 3, 4, 5}, khi đó tam giác được tạo nên như dưới đây:
Bài 22. Số nghiệm nguyên không âm (Microsoft) [C]. Cho hai số nguyên dương N và K. Hãy đếm số nghiệm nguyên không âm của phương trình x1+ x2 + x3 +…+xn = k. Ví dụ với n=4, k=1 thì số các nghiệm nguyên không âm của phương trình x1 + x2 + x3+ x4 = 1 là 4. Các nghiệm của phương trình bao gồm :(1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1).
Bài 23. Gray Code to Binay & Binary to Gray (Microsoft, Amazon) [A]. Số nhị phân được xem là cách mặc định biểu diễn các số. Tuy nhiên, trong nhiều ứng dụng của điện tử và truyền thông lại dùng một biến thể của mã nhị phân đó là mã Gray. Mã Gray độ dài n có mã đầu tiên là n số 0, mã kế tiếp của nó là một xâu nhị phân độ dài n khác biệt với xâu trước đó một bít. Ví dụ với n=3 ta có 23 mã Gray như sau: 000, 001, 011, 010, 110, 111, 101, 100. Hãy viết chương trình chuyển đổi một xâu mã nhị phân X có độ dài n thành một xâu mã Gray.
Tải về code C++
Tải về code C++(Giải thuật chia để trị)
Bài 19.Trong giờ học môn Điện tử số về mã Gray, MĐ chợt nảy sinh ra một bài toán để code. Bài toán rất đơn giản như sau: In ra lần lượt bảng mã gray n-bit.
Mã Gray là mã nhị phân mà hai mã liền kề trong bảng mã chỉ khác nhau một bit. Các giá trị ở nửa sau của bảng mã có sự đối xứng với nửa đầu của bảng mã theo thứ tự ngược lại, ngoại trừ bit cao nhất bị đảo giá trị (bit cao nhất là bit ngoài cùng bên trái). Tính chất đối xứng này vẫn đúng cho các bit thấp hơn trong mỗi nửa, mỗi phần tư,… của bảng mã.
Input
Một số nguyên duy nhất n (1<=n<=16).
Output
Bảng mã gray n-bit theo thứ tự, mỗi mã trên một dòng.
Tải về code C++
Bài 20.Cho số tự nhiên X.Hãy tìm cách biểu diễn X thành tổng lũy thừa bậc n của các số tự nhiên khác nhau.
Input: Output:
X=10,n=2 1 3
X=100,n=2 0 10
6 8
Tải về code C++
Bài 21.1. Special Triangle [A]. Cho dãy số A[] gồm n số nguyên dương. Tam giác đặc biệt của dãy số A[] là tam giác được tạo ra bởi n hàng, trong đó hàng thứ n là dãy số A[], hàng i là tổng hai phần tử liên tiếp của hàng i+1 (1≤i≤n-1). Ví dụ A[] = {1, 2, 3, 4, 5}, khi đó tam giác được tạo nên như dưới đây:
[48]
[20, 28]
[8, 12, 16]
[3, 5, 7, 9 ]
[1, 2, 3, 4, 5 ]
Hãy viết chương trình in ra tam giác đặc biệt của dãy số A[].
Tải về code C++Bài 22. Số nghiệm nguyên không âm (Microsoft) [C]. Cho hai số nguyên dương N và K. Hãy đếm số nghiệm nguyên không âm của phương trình x1+ x2 + x3 +…+xn = k. Ví dụ với n=4, k=1 thì số các nghiệm nguyên không âm của phương trình x1 + x2 + x3+ x4 = 1 là 4. Các nghiệm của phương trình bao gồm :(1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1).
Input: Output:
2 4
4 1 70
5 4
Tải về code C++Bài 23. Gray Code to Binay & Binary to Gray (Microsoft, Amazon) [A]. Số nhị phân được xem là cách mặc định biểu diễn các số. Tuy nhiên, trong nhiều ứng dụng của điện tử và truyền thông lại dùng một biến thể của mã nhị phân đó là mã Gray. Mã Gray độ dài n có mã đầu tiên là n số 0, mã kế tiếp của nó là một xâu nhị phân độ dài n khác biệt với xâu trước đó một bít. Ví dụ với n=3 ta có 23 mã Gray như sau: 000, 001, 011, 010, 110, 111, 101, 100. Hãy viết chương trình chuyển đổi một xâu mã nhị phân X có độ dài n thành một xâu mã Gray.
Dữ liệu vào:
· Dòng đầu tiên là số lượng test T (T≤100).
· T dòng kế tiếp ghi lại mỗi dòng một test. Mỗi test là một xâu nhị phân độ dài n (n≤100).
Kết quả ra của mỗi test được đưa ra trên một dòng tương ứng với mã Gray của test tương ứng.
Input: | Output: |
2 01001 01101 | 01101 01011 |
Bài 24. Gray Code to Binay & Binary to Gray (Microsoft, Amazon) [A]. Số nhị phân được xem là cách mặc định biểu diễn các số. Tuy nhiên, trong nhiều ứng dụng của điện tử và truyền thông lại dùng một biến thể của mã nhị phân đó là mã Gray. Mã Gray độ dài n có mã đầu tiên là n số 0, mã kế tiếp của nó là một xâu nhị phân độ dài n khác biệt với xâu trước đó một bít. Ví dụ với n=3 ta có 23 mã Gray như sau: 000, 001, 011, 010, 110, 111, 101, 100. Hãy viết chương trình chuyển đổi một xâu mã Gray X có độ dài n thành một xâu mã nhị phân.
Tải về code C++
Bài 25. Chia số trong xâu (Adopt)[C]. Cho một xâu ký tự bao gồm các chữ số. Hãy tìm tất cả các số có thể tạo ra bằng cách kết hợp các số trong xâu nhưng giữ nguyên vị trí. Ví dụ với xâu S[] =”123” ta sẽ có các cách tạo các số như sau:
Tải về code C++
Bài 26. Cho số tự nhiên n và k. Hãy viết chương trình liệt kê tất cả các tổ hợp chập k của 1, 2, .., n. Ghi chú, mỗi tổ hợp chập k của 1, 2, .., n tương ứng với một tập con k phần tử của 1, 2, .., n. Ví dụ với n = 5, k =3 ta có 10 tập con ba phần tử của 1, 2, 3, 4, 5 như dưới đây:
Tải về code C++
Bài 27. Cho hình chữ nhật gồm n´m hình vuông đơn vị. Hãy đếm số đường đi từ đỉnh của ô vuông cuối cùng góc trái lên đến đỉnh của ô vuông trên cùng góc phải. Biết mỗi bước đi ta chỉ được phép dịch sang phải hoặc lên trên theo các cạnh của hình vuông đơn vị.
Tải về code C++
Bài 28. Hãy viết chương trình liệt kê tất cả các hoán vị của 1, 2, .., n. Ví dụ với n = 4 sẽ cho ta 4! Hoán vị như dưới đây:
Tải về code C++
Bài 29. Hãy viết chương trình liệt kê tất cả các hoán vị của từ computer. Ví dụ từ computre là một hoán vị của từ compter.
Tải về code C++
Bài 30. Cho dãy số nguyên dương A[] = {a1, a2,.., an}. Hãy liệt kê tất cả các dãy số có thể tạo ra bằng cách tráo đổi các phần tử khác nhau của dãy số A[] sao cho tổng hai phần tử liên tiếp bất kỳ đều là một số nguyên tố. Dữ liệu vào cho bởi file data.in theo khuôn dạng:
Tải về code C++
Bài 31. Dãy sắp xếp tạo ra từ hai dãy sắp xếp (Microsoft). Cho hai dãy số đã được sắp xếp A[], B[]. Hãy in ra rất cả các dãy số đã được sắp xếp theo nguyên tắc: phần tử đầu tiên thuộc A[], phần tử tiếp theo thuộc B[]….
Bài 32. Giải bài toán cái túi bằng thuật toán qui hoạch động.
Bài 33. Tìm số các cách chia số tự nhiên n thành tổng các số tự nhiên nhỏ hơn n. Các cách chia là hoán vị của nhau chỉ được tính là một cách.
Bài 34. Thuật toán Brute-Force
Bài 35. Ban đầu cho một queue rỗng. Bạn cần thực hiện các truy vấn sau:
1. Trả về kích thước của queue
2. Kiểm tra xem queue có rỗng không, nếu có in ra “YES”, nếu không in ra “NO”.
3. Cho một số nguyên và đẩy số nguyên này vào cuối queue.
4. Loại bỏ phần tử ở đầu queue nếu queue không rỗng, nếu rỗng không cần thực hiện.
5. Trả về phần tử ở đầu queue, nếu queue rỗng in ra -1.
6. Trả về phần tử ở cuối queue, nếu queue rỗng in ra -1.
Dữ liệu vào
Dòng đầu tiên chứa số nguyên T là số bộ dữ liệu, mỗi bộ dữ theo dạng sau.
Dòng đầu tiên chứa số nguyên n - lượng truy vấn (1 ≤ n ≤ 1000)
N dòng tiếp theo, mỗi dòng sẽ ghi loại truy vấn như trên, với truy vấn loại 3 sẽ có thêm một số nguyên, không quá 106.
Kết quả: In ra kết quả của các truy vấn..
Ví dụ:
Input Output
1 1
14 3
3 1 5
3 2 2
3 3
5
6
4
4
4
4
4
3 5
3 6
5
1
Bài 36. Yêu cầu bạn xây dựng một queue với các truy vấn sau đây:
“PUSH x”: Thêm phần tử x vào cuối của queue (0 ≤ x ≤ 1000).
“PRINTFRONT”: In ra phần tử đầu tiên của queue. Nếu queue rỗng, in ra “NONE”.
Bài 37. Cho hai số nguyên tố khác nhau có bốn chữ số. Người ta cho rằng hoàn toàn có thể biến đổi từ số này thành số kia sau một số bước theo quy tắc: Tại mỗi bước ta chỉ thay đổi một chữ số trong số trước đó sao cho số tạo được trong mỗi bước đều là một số nguyên tố có bốn chữ số. Một cách biến đổi như vậy gọi là một “đường nguyên tố”. Bài toán đặt ra là với một cặp số nguyên tố đầu vào, hãy tính ra số bước của đường nguyên tố ngắn nhất.
Giả sử đầu vào là hai số 1033 và 8179 thì đường nguyên tố ngắn nhất sẽ có độ dài là 6 với các bước chuyển là: 1033 1733 3733 3739 3779 8779 8179
Dữ liệu vào: Dòng đầu tiên ghi số bộ test, không lớn hơn 100. Mỗi bộ test viết trên một dòng bao gồm hai số nguyên tố có 4 chữ số..
Kết quả: Với mỗi bộ test, in ra màn hình trên một dòng số bước của đường nguyên tố ngắn nhất.
Ví dụ:
Input Output
3 6
1033 7
8179 0
1373
8017
1033
1033
Bài 38. Có một chiếc bảng hình chữ nhật với 6 miếng ghép, trên mỗi miếng ghép được điền một số nguyên trong khoảng từ 1 đến 6. Tại mỗi bước, chọn một hình vuông (bên trái hoặc bên phải), rồi quay theo chiều kim đồng hồ.
Bài 39. Cho một bảng kích thước N x N, trong đó có các ô trống ‘.’ và vật cản ‘X’. Các hàng và các cột được đánh số từ 0. Mỗi bước di chuyển, bạn có thể đi từ ô (x, y) tới ô (u, v) nếu như 2 ô này nằm trên cùng một hàng hoặc một cột, và không có vật cản nào ở giữa. Cho điểm xuất phát và điểm đích. Bạn hãy tính số bước di chuyển ít nhất? Dữ liệu vào: Dòng đầu tiên là số nguyên dương N (1 ≤ N ≤ 100). N dòng tiếp theo, mỗi dòng gồm N kí tự mô tả bảng. Cuối cùng là 4 số nguyên a, b, c, d với (a, b) là tọa độ điểm xuất phát, (c, d) là tọa độ đích. Dữ liệu đảm bảo hai vị trí này không phải là ô cấm. Kết quả: In ra một số nguyên là đáp số của bài toán.
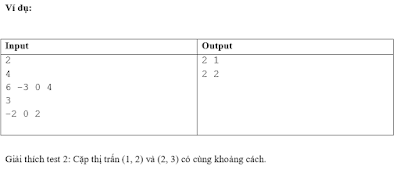
Bài 39. Thành phố X có N thị trấn trên trục đường chính. Tọa độ của các thị trấn lần lượt là a[1], a[2], …, a[N], các tọa độ này là phân biệt, không có 2 tọa độ nào trùng nhau.
Chính quyền thành phố muốn xây dựng một tuyến buýt nhanh BRT để kết nối 2 thị trấn gần nhau nhất với nhau.
Bạn hãy tính thử xem chiều dài của tuyến buýt này bằng bao nhiêu? Và có bao nhiêu cặp thị trấn có tiềm năng giống nhau để xây dựng tuyến BRT này.
Dữ liệu vào: Dòng đầu tiên là số lượng bộ test T (T ≤ 10).
Mỗi test bắt đầu bằng số nguyên N (N ≤ 100 000). Dòng tiếp theo gồm N số nguyên A[i] (-109 ≤ A[i] ≤ 109).
Kết quả:
Với mỗi test in ra 2 số nguyên C và D, lần lượt là khoảng cách ngắn nhất giữa 2 thị trấn, và số lượng cặp thị trấn có cùng khoảng cách ngắn nhất này.
Bài 40. Xây dựng các thao tác cơ bản trên danh sách liên kết đơn(C++), bao gồm:
• Khởi tạo danh sách liên kết đơn.
• Chèn node vào đầu danh sách liên kết đơn.
• Chèn node vào cuối danh sách liên kết đơn.
• Chèn node vào vị trí xác định trong danh sách liên kết đơn.
• Loại node tại vị trí Pos trong danh sách liên kết đơn.
• Sửa đổi nội dung node trong danh sách liên kết đơn.
• Sắp xếp các node của danh sách liên kết đơn.
• Đảo ngược các node trong danh sách liên kết đơn.
• Tìm kiếm vị trí của node trong danh sách liên kết đơn.
• Hiển thị nội dung trong danh sách liên kết đơn.
Bài 41. Thuật toán chuyển đổi biểu thức trung tố P thành biểu thức hậu tố?(Sử dụng ngăn xếp)
VD:
Dữ liệu vào:
· Dòng đầu tiên là số lượng test T (T≤100).
· T dòng kế tiếp ghi lại mỗi dòng một test. Mỗi test là một xâu mã Gray độ dài n (n≤100).
Kết quả ra của mỗi test được đưa ra trên một dòng tương ứng với mã nhị phân của test tương ứng.
Input: | Output: |
2 01101 01011 | 01001 01101 |
Bài 25. Chia số trong xâu (Adopt)[C]. Cho một xâu ký tự bao gồm các chữ số. Hãy tìm tất cả các số có thể tạo ra bằng cách kết hợp các số trong xâu nhưng giữ nguyên vị trí. Ví dụ với xâu S[] =”123” ta sẽ có các cách tạo các số như sau:
1 2 3 23 12 123
Bài 26. Cho số tự nhiên n và k. Hãy viết chương trình liệt kê tất cả các tổ hợp chập k của 1, 2, .., n. Ghi chú, mỗi tổ hợp chập k của 1, 2, .., n tương ứng với một tập con k phần tử của 1, 2, .., n. Ví dụ với n = 5, k =3 ta có 10 tập con ba phần tử của 1, 2, 3, 4, 5 như dưới đây:
N=5, k = 3 | |
1 2 3 1 2 4 1 2 5 1 3 4 1 3 5 1 4 5 2 3 4 2 3 5 2 4 5 |
Tải về code C++
Bài 27. Cho hình chữ nhật gồm n´m hình vuông đơn vị. Hãy đếm số đường đi từ đỉnh của ô vuông cuối cùng góc trái lên đến đỉnh của ô vuông trên cùng góc phải. Biết mỗi bước đi ta chỉ được phép dịch sang phải hoặc lên trên theo các cạnh của hình vuông đơn vị.
Dữ liệu vào cho bởi file data.in theo khuôn dạng:
· Dòng đầu tiên ghi lại số T tương ứng với số lượng test.
· T dòng kế tiếp, mỗi dòng ghi lại một test. Mỗi test là một bộ đôi n, m tương ứng với hình chữ nhật gồm n´m hình vuông đơn vị.
Kết quả ra ghi lại trong file ketqua.out theo từng dòng ứng với mỗi test. Ví dụ dưới đây sẽ minh họa cho file data.in và ketqua.out của bài toán.
Data.in | Ketqua.out |
3 5 3 6 3 7 4 | 10 20 35 |
Bài 28. Hãy viết chương trình liệt kê tất cả các hoán vị của 1, 2, .., n. Ví dụ với n = 4 sẽ cho ta 4! Hoán vị như dưới đây:
N=4 | |
1 2 3 4 1 2 4 3 1 3 2 4 1 3 4 2 1 4 2 3 1 4 3 2 2 1 3 4 2 1 4 3 2 3 1 4 2 3 4 1 2 4 1 3 2 4 3 1 | 3 1 2 4 3 1 4 2 3 2 1 4 3 2 4 1 3 4 1 2 3 4 2 1 4 1 2 3 4 1 3 2 4 2 1 3 4 2 3 1 4 3 1 2 2 3 2 1 |
Tải về code C++
Bài 29. Hãy viết chương trình liệt kê tất cả các hoán vị của từ computer. Ví dụ từ computre là một hoán vị của từ compter.
Tải về code C++
Bài 30. Cho dãy số nguyên dương A[] = {a1, a2,.., an}. Hãy liệt kê tất cả các dãy số có thể tạo ra bằng cách tráo đổi các phần tử khác nhau của dãy số A[] sao cho tổng hai phần tử liên tiếp bất kỳ đều là một số nguyên tố. Dữ liệu vào cho bởi file data.in theo khuôn dạng:
· Dòng đầu tiên ghi lại số tự nhiên n là số phần tử của dãy số A[].
· Dòng kế tiếp ghi lại các phần tử của dãy số A[].
Các dãy số thỏa mã yêu cầu của bài toán ghi lại trong file ketqua.out, mỗi dãy số được ghi trên một dòng. Ví dụ dưới đây sẽ minh họa cho file data.in và ketqua.out của bài toán.
Data.in | Kequa.out |
6 9 7 12 8 6 5 | 6 7 12 5 8 9 9 8 5 6 7 12 9 8 5 12 7 6 12 7 6 5 8 9 |
Bài 31. Dãy sắp xếp tạo ra từ hai dãy sắp xếp (Microsoft). Cho hai dãy số đã được sắp xếp A[], B[]. Hãy in ra rất cả các dãy số đã được sắp xếp theo nguyên tắc: phần tử đầu tiên thuộc A[], phần tử tiếp theo thuộc B[]….
Ví dụ với dãy A[] = {10, 15, 25}, B[] = {1, 5, 20, 30 } ta sẽ có các dãy số được tạo ra theo nguyên tắc trên như sau:
10 20
10 20 25 30
10 30
15 20
15 20 25 30
15 30
25 30
Bài 32. Giải bài toán cái túi bằng thuật toán qui hoạch động.
Bài 33. Tìm số các cách chia số tự nhiên n thành tổng các số tự nhiên nhỏ hơn n. Các cách chia là hoán vị của nhau chỉ được tính là một cách.
Bài 34. Thuật toán Brute-Force
Bài 35. Ban đầu cho một queue rỗng. Bạn cần thực hiện các truy vấn sau:
1. Trả về kích thước của queue
2. Kiểm tra xem queue có rỗng không, nếu có in ra “YES”, nếu không in ra “NO”.
3. Cho một số nguyên và đẩy số nguyên này vào cuối queue.
4. Loại bỏ phần tử ở đầu queue nếu queue không rỗng, nếu rỗng không cần thực hiện.
5. Trả về phần tử ở đầu queue, nếu queue rỗng in ra -1.
6. Trả về phần tử ở cuối queue, nếu queue rỗng in ra -1.
Dữ liệu vào
Dòng đầu tiên chứa số nguyên T là số bộ dữ liệu, mỗi bộ dữ theo dạng sau.
Dòng đầu tiên chứa số nguyên n - lượng truy vấn (1 ≤ n ≤ 1000)
N dòng tiếp theo, mỗi dòng sẽ ghi loại truy vấn như trên, với truy vấn loại 3 sẽ có thêm một số nguyên, không quá 106.
Kết quả: In ra kết quả của các truy vấn..
Ví dụ:
Input Output
1 1
14 3
3 1 5
3 2 2
3 3
5
6
4
4
4
4
4
3 5
3 6
5
1
Bài 36. Yêu cầu bạn xây dựng một queue với các truy vấn sau đây:
“PUSH x”: Thêm phần tử x vào cuối của queue (0 ≤ x ≤ 1000).
“PRINTFRONT”: In ra phần tử đầu tiên của queue. Nếu queue rỗng, in ra “NONE”.
“POP”: Xóa phần tử ở đầu của queue. Nếu queue rỗng, không làm gì cả.
Dữ liệu vào: Dòng đầu tiên là số lượng truy vấn Q (Q ≤ 100000). Mỗi truy vấn có dạng như trên.
Kết quả: Với mỗi truy vấn “PRINT”, hãy in ra phần tử đầu tiên của queue. Nếu queue rỗng, in ra “NONE”. Ví dụ:
Input: Output:
9 2
PUSH 1 2
PUSH 2 NONE
POP
PRINTFRONT
PUSH 3
PRINTFRONT
POP
POP
PRINTFRONT
Bài 37. Cho hai số nguyên tố khác nhau có bốn chữ số. Người ta cho rằng hoàn toàn có thể biến đổi từ số này thành số kia sau một số bước theo quy tắc: Tại mỗi bước ta chỉ thay đổi một chữ số trong số trước đó sao cho số tạo được trong mỗi bước đều là một số nguyên tố có bốn chữ số. Một cách biến đổi như vậy gọi là một “đường nguyên tố”. Bài toán đặt ra là với một cặp số nguyên tố đầu vào, hãy tính ra số bước của đường nguyên tố ngắn nhất.
Giả sử đầu vào là hai số 1033 và 8179 thì đường nguyên tố ngắn nhất sẽ có độ dài là 6 với các bước chuyển là: 1033 1733 3733 3739 3779 8779 8179
Dữ liệu vào: Dòng đầu tiên ghi số bộ test, không lớn hơn 100. Mỗi bộ test viết trên một dòng bao gồm hai số nguyên tố có 4 chữ số..
Kết quả: Với mỗi bộ test, in ra màn hình trên một dòng số bước của đường nguyên tố ngắn nhất.
Ví dụ:
Input Output
3 6
1033 7
8179 0
1373
8017
1033
1033
Bài 38. Có một chiếc bảng hình chữ nhật với 6 miếng ghép, trên mỗi miếng ghép được điền một số nguyên trong khoảng từ 1 đến 6. Tại mỗi bước, chọn một hình vuông (bên trái hoặc bên phải), rồi quay theo chiều kim đồng hồ.
Yêu cầu: Cho một trạng thái của bảng, hãy tính số phép biến đổi ít nhất để đưa bảng đến trạng thái đích.
Dữ liệu vào: Dòng đầu tiên chứa 6 số là trạng thái bảng ban đầu (thứ tự từ trái qua phải, dòng 1 tới dòng 2).
Dòng thứ hai chứa 6 số là trạng thái bảng đích (thứ tự từ trái qua phải, dòng 1 tới dòng 2).
Kết quả: In ra một số nguyên là đáp số của bài toán.
Ví dụ:
Input: Output:
1 2 3 4 5 6 2
4 1 2 6 5 3
Bài 39. Cho một bảng kích thước N x N, trong đó có các ô trống ‘.’ và vật cản ‘X’. Các hàng và các cột được đánh số từ 0. Mỗi bước di chuyển, bạn có thể đi từ ô (x, y) tới ô (u, v) nếu như 2 ô này nằm trên cùng một hàng hoặc một cột, và không có vật cản nào ở giữa. Cho điểm xuất phát và điểm đích. Bạn hãy tính số bước di chuyển ít nhất? Dữ liệu vào: Dòng đầu tiên là số nguyên dương N (1 ≤ N ≤ 100). N dòng tiếp theo, mỗi dòng gồm N kí tự mô tả bảng. Cuối cùng là 4 số nguyên a, b, c, d với (a, b) là tọa độ điểm xuất phát, (c, d) là tọa độ đích. Dữ liệu đảm bảo hai vị trí này không phải là ô cấm. Kết quả: In ra một số nguyên là đáp số của bài toán.
Bài 39. Thành phố X có N thị trấn trên trục đường chính. Tọa độ của các thị trấn lần lượt là a[1], a[2], …, a[N], các tọa độ này là phân biệt, không có 2 tọa độ nào trùng nhau.
Chính quyền thành phố muốn xây dựng một tuyến buýt nhanh BRT để kết nối 2 thị trấn gần nhau nhất với nhau.
Bạn hãy tính thử xem chiều dài của tuyến buýt này bằng bao nhiêu? Và có bao nhiêu cặp thị trấn có tiềm năng giống nhau để xây dựng tuyến BRT này.
Dữ liệu vào: Dòng đầu tiên là số lượng bộ test T (T ≤ 10).
Mỗi test bắt đầu bằng số nguyên N (N ≤ 100 000). Dòng tiếp theo gồm N số nguyên A[i] (-109 ≤ A[i] ≤ 109).
Kết quả:
Với mỗi test in ra 2 số nguyên C và D, lần lượt là khoảng cách ngắn nhất giữa 2 thị trấn, và số lượng cặp thị trấn có cùng khoảng cách ngắn nhất này.
Bài 40. Xây dựng các thao tác cơ bản trên danh sách liên kết đơn(C++), bao gồm:
• Khởi tạo danh sách liên kết đơn.
• Chèn node vào đầu danh sách liên kết đơn.
• Chèn node vào cuối danh sách liên kết đơn.
• Chèn node vào vị trí xác định trong danh sách liên kết đơn.
• Loại node tại vị trí Pos trong danh sách liên kết đơn.
• Sửa đổi nội dung node trong danh sách liên kết đơn.
• Sắp xếp các node của danh sách liên kết đơn.
• Đảo ngược các node trong danh sách liên kết đơn.
• Tìm kiếm vị trí của node trong danh sách liên kết đơn.
• Hiển thị nội dung trong danh sách liên kết đơn.
Bài 41. Thuật toán chuyển đổi biểu thức trung tố P thành biểu thức hậu tố?(Sử dụng ngăn xếp)
VD:
Infix | Postfix |
A / B – C * D | A B / C D * + |
A / ( B – C * D) | A B C D * - / |
A / (B – C) * D | A B C - / D * |



0 nhận xét:
Đăng nhận xét